Chair's Message
Dear Alumni and Friends of the Department of Mathematics:
In this issue of By the Numb3rs you can read about recent developments in the Department as well as some accomplishments by our students and faculty. We are pleased to inform you that Dr. Michael Neilan has won the Leslie Fox Prize in Numerical Analysis. Dr. Jonathan Rubin recently spent his sabbatical working on a research project in New Zealand at the University of Auckland. Undergraduate students are working with Dr. Bard Ermentrout on several interesting projects and Jeff Connors, Ph.D., class of 2010, has accepted a tenure-track Assistant Professor position at the University of Connecticut.
We are pleased to share with you that our faculty received three new research awards from the National Science Foundation. We have highlighted some of the excellent research being done by Dr. Neilan in computational and applied mathematics with an emphasis on numerical methods for partial differential equations, in particular, finite elements methods. With the continued support of the Math Research Center, with generous funding from the Dietrich School of Arts and Sciences, we have organized several workshops and conference and several more are scheduled for the Spring 2014 term.
We have changes and additions to our department. Dr. Paul Gartside has stepped down as Graduate Director after 4 years of dedicated service. We'd like to extend our thanks for his hard work and dedication as Graduate Director. Dr. David Swigon has been named as the new Graduate Director. Dr. Hao Xu joins us as a new Assistant Professor and Ms. Pat Markham joins us as the Graduate Student Administrator.
As always, please keep in touch. We would love to hear from you. Visit our web page www.mathematics.pitt.edu for information on how to contact us and for the latest news about the Department.
Sincerely yours,
Ivan Yotov, Chair
Department of Mathematics
Assistant Professor Michael Neilan wins the Leslie Fox Prize
On June 24, 2013 Michael Neilan won the Leslie Fox Prize in numerical analysis with the talk, "Conforming and divergence-free Stokes elements on general triangular meshes." This talk is based on the paper joint with Johnny Guzman (Brown University) with a similar title appearing in the journal Mathematics of Computations.
 The Leslie Fox Prize for Numerical Analysis of the Institute of Mathematics and its Applications (IMA) is a biennial prize established in 1985 by the IMA in honour of mathematician Leslie Fox (1918-1992). The prize honours "young numerical analysts worldwide" (any person who is less than 31 years old), and applicants submit papers for review. A committee reviews the papers, invites shortlisted candidates to give lectures at the Leslie Fox Prize meeting, and then awards First Prize and Second Prizes based on "mathematical and algorithmic brilliance in tandem with presentational skills.
The Leslie Fox Prize for Numerical Analysis of the Institute of Mathematics and its Applications (IMA) is a biennial prize established in 1985 by the IMA in honour of mathematician Leslie Fox (1918-1992). The prize honours "young numerical analysts worldwide" (any person who is less than 31 years old), and applicants submit papers for review. A committee reviews the papers, invites shortlisted candidates to give lectures at the Leslie Fox Prize meeting, and then awards First Prize and Second Prizes based on "mathematical and algorithmic brilliance in tandem with presentational skills.
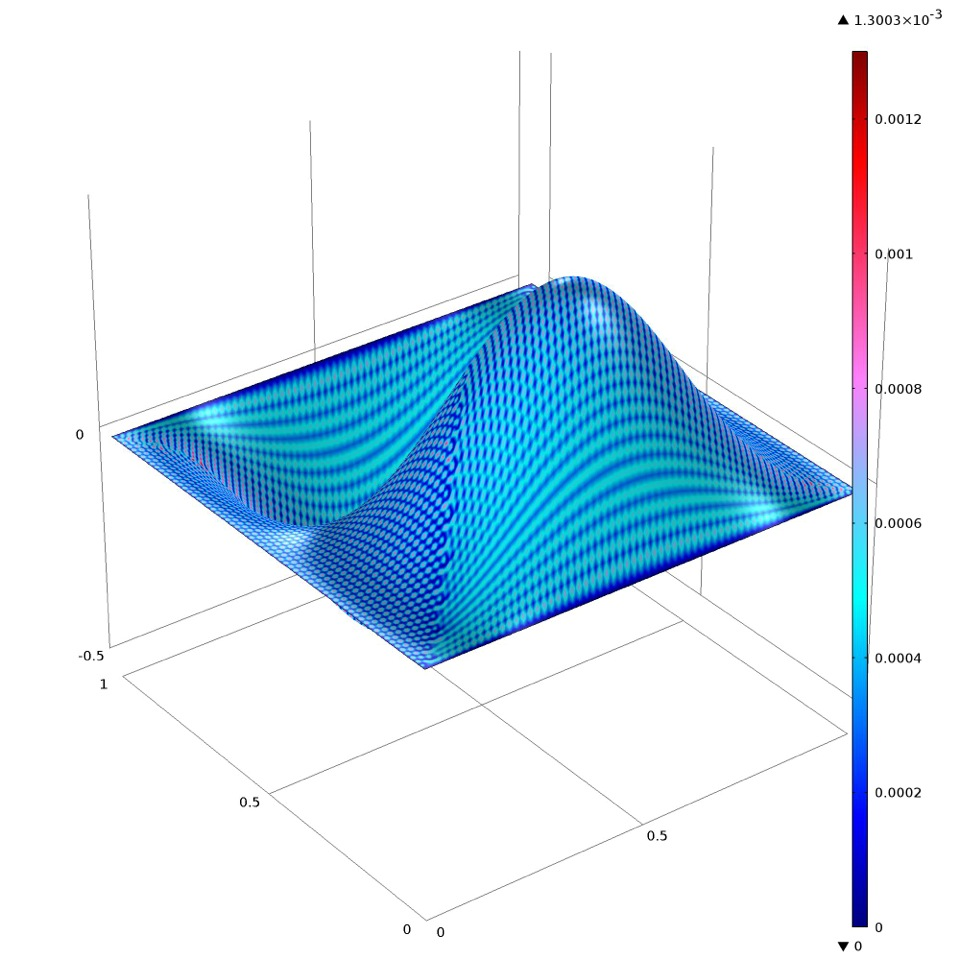
The overall theme of this work was to design numerical methods that closely mimic the physical and mathematical structures of the underlying system of equations describing the motion of fluids, in particular, the Stokes/Navier-Stokes equations. These partial differential equations are ubiquitous in mod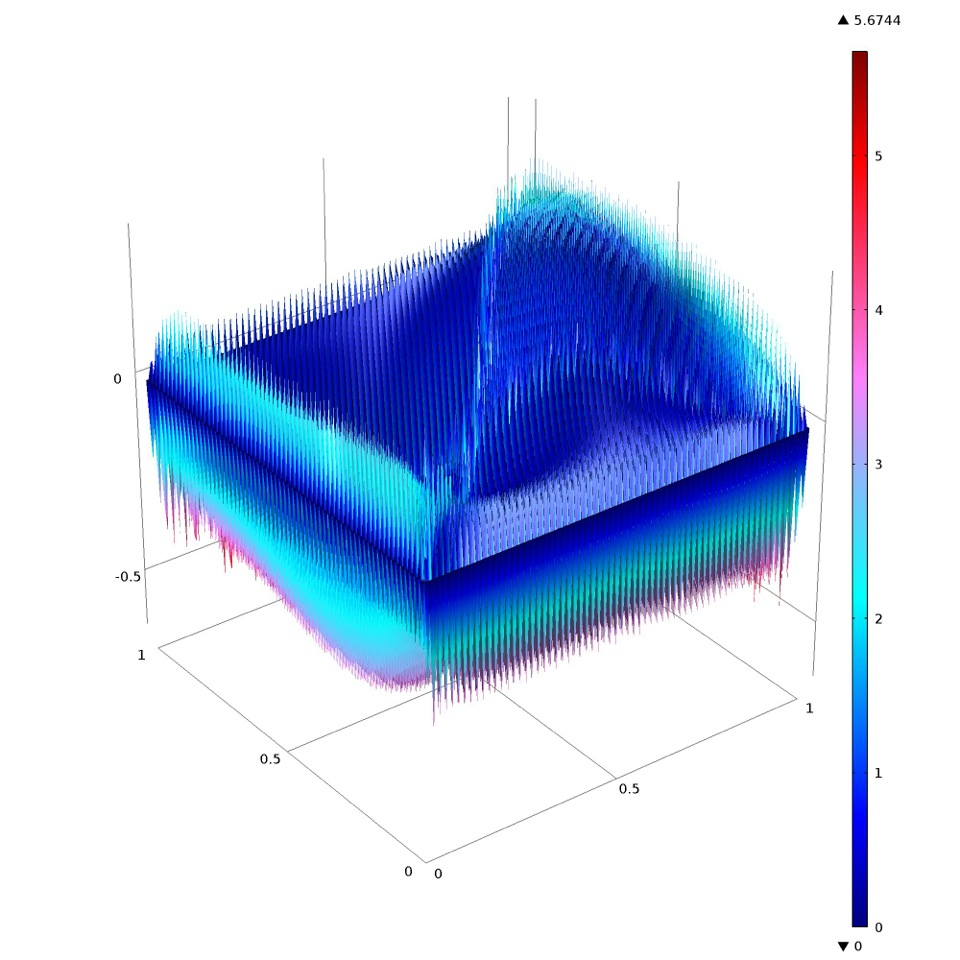 els for, e.g., weather prediction, air flow around the wing of an aircraft, blood flow, and ocean currents. In their simplest form, these equations describe how the velocity and pressure of a fluid are related under the constraints of conservation of mass and conservation of momentum.
els for, e.g., weather prediction, air flow around the wing of an aircraft, blood flow, and ocean currents. In their simplest form, these equations describe how the velocity and pressure of a fluid are related under the constraints of conservation of mass and conservation of momentum.
Except for simple and unrealistic settings the Stokes problem cannot be solved in closed form and computational methods are the only viable way to compute (approximate) solutions. The finite element method is an established and ubiquitous tool to solve partial differential equations, and these methods have been developed for  the Stokes problem for over 40 years. Finite element methods for the Stokes problem generally fall into the class of mixed methods, where two or more finite dimensional subspaces are utilized to compute the solution. It is well-known that the spaces must be compatible to ensure a stable method; in particular, the so-called inf-sup condition must be satisfied to ensure the well-posedness of the discretization. While the construction of inf-sup stable schemes is non-trivial, many pairs of finite element spaces satisfying the condition have been developed and used in practice for the Stokes problem. However, all of these schemes relax the physical properties of the model, namely, the conservation of mass (i.e., incompressibility of the fluid) is only enforced weakly. The lack of strict enforcement of this condition has been shown to have dramatic consequences with respect to accuracy and physical relevance, even at small Reynolds numbers.
the Stokes problem for over 40 years. Finite element methods for the Stokes problem generally fall into the class of mixed methods, where two or more finite dimensional subspaces are utilized to compute the solution. It is well-known that the spaces must be compatible to ensure a stable method; in particular, the so-called inf-sup condition must be satisfied to ensure the well-posedness of the discretization. While the construction of inf-sup stable schemes is non-trivial, many pairs of finite element spaces satisfying the condition have been developed and used in practice for the Stokes problem. However, all of these schemes relax the physical properties of the model, namely, the conservation of mass (i.e., incompressibility of the fluid) is only enforced weakly. The lack of strict enforcement of this condition has been shown to have dramatic consequences with respect to accuracy and physical relevance, even at small Reynolds numbers.
In the Leslie Fox Talk, Dr. Neilan discussed the first class of finite element spaces for the Stokes problem that are both inf-sup stable and satisfy the incompressibility condition exactly on general simplicial partitions. The key idea in the construction is to use cohomological techniques with a discrete smooth de Rham complex as their main tool. Starting with a class of H2 conforming finite element spaces developed 45 years ago, Neilan and Guzman used the complex as a guide to construct finite element pairs with the desired properties.
Prof. Rubin Travels to New Zealand for Sabatical
New Zeala nd historically has been easy to miss, remaining essentially uninhabited until less than 1000 years ago and free from European settlement until the 1700’s. While its history is relatively recent and its population is under 4.5 million (vs. over 80 million in Germany in a similar land area), New Zealand nonetheless is home to some significant Mathematics activities, as I was fortunate enough to find out first hand while at the University of Auckland on sabbatical over the first six months of 2013.
nd historically has been easy to miss, remaining essentially uninhabited until less than 1000 years ago and free from European settlement until the 1700’s. While its history is relatively recent and its population is under 4.5 million (vs. over 80 million in Germany in a similar land area), New Zealand nonetheless is home to some significant Mathematics activities, as I was fortunate enough to find out first hand while at the University of Auckland on sabbatical over the first six months of 2013.
The Department of Mathematics at the University of Auckland provided an excellent setting for sabbatical research combining a mathematical focus together with relevance to biological systems. The department boasts a first‐class, highly active applied dynamical systems group. Both discrete and continuous dynamics are represented, and the group even has a healthy interaction with the department’s topologists on the study of various complex mappings and manifold structures. Most of its members have some interest in biological dynamics, engaging in interdisciplinary collaborations while maintaining an emphasis on mathematical issues, which was exactly what I was seeking for my sabbatical.
 During my visit to Auckland, I started two new research projects. One project, on multiple time scale dynamics, was a collaboration with faculty member Vivien Kirk and her graduate student Pingyu Nan, along with Pitt graduate student Yangyang Wang, who was able to visit for almost three months as well. The other project, on an activity pattern known as bursting, was done with the dynamic duo of Brent Krauskopf and Hinke Osinga, faculty members who were recently recruited from Bristol to Auckland and are well-known for, among other things, crocheting the Lorenz manifold (Mathematical Intelligencer, 2004).
During my visit to Auckland, I started two new research projects. One project, on multiple time scale dynamics, was a collaboration with faculty member Vivien Kirk and her graduate student Pingyu Nan, along with Pitt graduate student Yangyang Wang, who was able to visit for almost three months as well. The other project, on an activity pattern known as bursting, was done with the dynamic duo of Brent Krauskopf and Hinke Osinga, faculty members who were recently recruited from Bristol to Auckland and are well-known for, among other things, crocheting the Lorenz manifold (Mathematical Intelligencer, 2004).
The starting point for the multiple time scale project is the observation that interacting biological processes often  evolve on disparate time scales. It is common practice to group variables in models of such systems into fast and slow subsystems and to exploit their separation to attain analytical insights about solution behavior. In our work, we are examining the implications of allowing a third, superslow variable class. We have identified certain solution properties that require three distinct scales and explained how they emerge. Our findings will help researchers in the future to decide what model features are important for capturing their empirical observations.
evolve on disparate time scales. It is common practice to group variables in models of such systems into fast and slow subsystems and to exploit their separation to attain analytical insights about solution behavior. In our work, we are examining the implications of allowing a third, superslow variable class. We have identified certain solution properties that require three distinct scales and explained how they emerge. Our findings will help researchers in the future to decide what model features are important for capturing their empirical observations.
In the bursting project, we are considering systems with more traditional two time scale separation. The systems we study generate outputs known as bursts, featuring phases of rapid oscillations alternating with quiet phases of little activity. Bursts in some neurons help to generate basic activity such as breathing, and bursts also can show up in certain neural diseases. Typically, one part of fast-‐slow analysis is to treat a slow variable as a parameter and to consider how the behaviors of fast variables change as this parameter is varied. Aided by computer simulations, we carried out a version of this approach aimed at fitting the output of a model system with two slow variables to experimentally observed bursting patterns. The idea is that we can first find a curve in two‐slow-variable space such that forcing the slow variables to travel along this curve causes the fast variables to generate the patterns that we want, and then we can find parameters that cause the slow variables to follow close to this curve on their own. As a result, we can use the fast‐slow time scale separation to gain efficiency in fitting model behaviors to data.
Another major challenge of the visit had more to do with time zones than time scales: moving a family of four,  including 10 and 13 year old boys, 8500 miles around the globe! There were some significant hurdles to clear before we could set out for mighty Aoteoroa, such as finding housing, figuring out a school plan, and many others. But the payoff was easily worth the effort. It is difficult to do justice to the beauty of the country or to all of the amazing things we saw there. New Zealand’s origins are volcanic, and Auckland is home to dozens of dormant volcanoes (often with sheep or cows grazing on their slopes), with beautiful views of the surrounding harbors visible from all over the city. Outside of Auckland, we enjoyed wandering New Zealand’s coastlines, playing in its waves, and strolling through its towering, bird-‐filled forests. We visited the less populated South Island in the summer (in January!), where we found wild seals, sea lions, and penguins wading along the coasts. Even in popular tourist areas in high season, we could drive the scenic, winding roads for hours and only see a handful of cars. We were also able to travel quite a bit during off‐peak times and explore many spots at our own pace. We especially enjoyed a quiet northern trip in May, where we explored Maori culture, were awed by the mighty kauri trees, and saw the Tasman Sea and Pacific Ocean crashing into each other at the nation’s northwestern tip.
including 10 and 13 year old boys, 8500 miles around the globe! There were some significant hurdles to clear before we could set out for mighty Aoteoroa, such as finding housing, figuring out a school plan, and many others. But the payoff was easily worth the effort. It is difficult to do justice to the beauty of the country or to all of the amazing things we saw there. New Zealand’s origins are volcanic, and Auckland is home to dozens of dormant volcanoes (often with sheep or cows grazing on their slopes), with beautiful views of the surrounding harbors visible from all over the city. Outside of Auckland, we enjoyed wandering New Zealand’s coastlines, playing in its waves, and strolling through its towering, bird-‐filled forests. We visited the less populated South Island in the summer (in January!), where we found wild seals, sea lions, and penguins wading along the coasts. Even in popular tourist areas in high season, we could drive the scenic, winding roads for hours and only see a handful of cars. We were also able to travel quite a bit during off‐peak times and explore many spots at our own pace. We especially enjoyed a quiet northern trip in May, where we explored Maori culture, were awed by the mighty kauri trees, and saw the Tasman Sea and Pacific Ocean crashing into each other at the nation’s northwestern tip.
After six months in New Zealand, we exchanged islands and accents, moving on for a month in Australia. We spent most of that time in Sydney, where I worked with Martin Wechselberger at the University of Sydney on a ma thematical follow up to some earlier work we had done on bursting in a respiratory neuron model. We soon became convinced that our terraced rental house was haunted, and we learned that insulation has not made it to the Southern Hemisphere, but we had a great time nonetheless. In addition to exploring Sydney, we traveled to Kakadu National Park, where we had a close up introduction to Cleft and Fang (5 meter saltwater crocs in the Adelaide River), toured aboriginal rock art sites, and ate bush tucker in a billabong at sunset. We also voyaged to Cairns, where we snorkeled at the Great Barrier Reef and saw a pair of elusive dagger-‐clawed cassowaries in the rainforest. Before we knew it though, it was time to say “Kia Ora” to the land Down Under and to return to Pittsburgh and Thackeray Hall.
thematical follow up to some earlier work we had done on bursting in a respiratory neuron model. We soon became convinced that our terraced rental house was haunted, and we learned that insulation has not made it to the Southern Hemisphere, but we had a great time nonetheless. In addition to exploring Sydney, we traveled to Kakadu National Park, where we had a close up introduction to Cleft and Fang (5 meter saltwater crocs in the Adelaide River), toured aboriginal rock art sites, and ate bush tucker in a billabong at sunset. We also voyaged to Cairns, where we snorkeled at the Great Barrier Reef and saw a pair of elusive dagger-‐clawed cassowaries in the rainforest. Before we knew it though, it was time to say “Kia Ora” to the land Down Under and to return to Pittsburgh and Thackeray Hall.
Featured Alumni
Jeffrey Connors, PhD 2010
Jeffrey Connors finished a position as a postdoctoral research associate at Lawrence Livermore National Laboratory (LLNL) over the summer and started a tenure-track professorship at the University of Connecticut - Avery Point campus in the department of Mathematics. At LLNL he has been focusing on methods to calculate estimates of numerical errors for multi-physics computer simulations to help understand uncertainties in simulation outputs. Now that he has started as a professor at University of Connecticut, he will continue some of this work but will focus more on the problem of numerical modeling of atmosphere-ocean interaction.
Undergrate Research
Cutaneous Rabbit
Dr. Bard Ermentrount is working with Evan Cresswell, a senior Mathematics Undergraduate Major on the Cutaneous Rabbit. The illusion called the cutaneous rabbit, works as follows. A subject is tapped two times on the wrist and a third time at the crook of the elbow. His eyes are covered. The illusion is that the second tap is felt somewhere between the wrist and the upper forearm. There have been a few very abstract models of this using priors and Bayesian inference.
Ermentrout and Cresswell created a mechanistic model for this illusion. The model is based on a neural network representing the spatial location on the arm. This is coupled with a second process that recognized what the stimulus was but this has a delay associated with it. The delayed recognition of the "what" coupled with the rapid recognition of "where" gives the illusion of the location of the second tap to be somewhere in between depending on the timing. The model is able to fit psychophysical data. They are now trying to see how the illusion depends on different parameters in the model. Cresswell will present this work in the form of a poster at a math meeting in January 2014.
First Experiences in Research
Sophomore neuroscience major, Sarah Miller is continuing to work on a project started in the Spring term as part of the First Experiences in Research (she liked it enough that she wanted to continue). This project is a bit more abstract than the others. Here She and Dr. Ermentrout are looking at the dynamics of locally connected oscillators in square and cubic lattices. Such networks will frequently synchronize, but can also produce more exotic patterns such as rotating waves and various other complicated patterns. Last semester they characterized all the nonsynchronous patterns in 6x6 and 8x8 arrays of oscillators. They are now trying to understand the patterns that occur in NxNxN arrays for small N. The motive for this is that such nonsynchronous dynamics is seen in two-dimensions in various experimentally induced seizures on slabs of cortical tissue and three-dimensional waves are seen during arrythmias in the heart.