Research
Collaborative Research in Computational Neuroscience (CRCNS)
In the summer of 2015, Dr. Jonathan Rubin and Dr. Brent Doiron both received new grants through the Collaborative Research in Computational Neuroscience (CRCNS) program. As the name suggests, these awards support joint efforts between theorists and experimentalists to address important problems in neuroscience. They are funded by multiple sources, including the National Science Foundation (NSF) and the National Institutes of Health (NIH). The impetus behind the CRCNS program is the belief that understanding structure, computation, function, and dysfunction in the nervous system requires an interdisciplinary approach and that, thanks to recent advances in theory, experiment, and computing power, the time is now right to make significant progress on these problems.
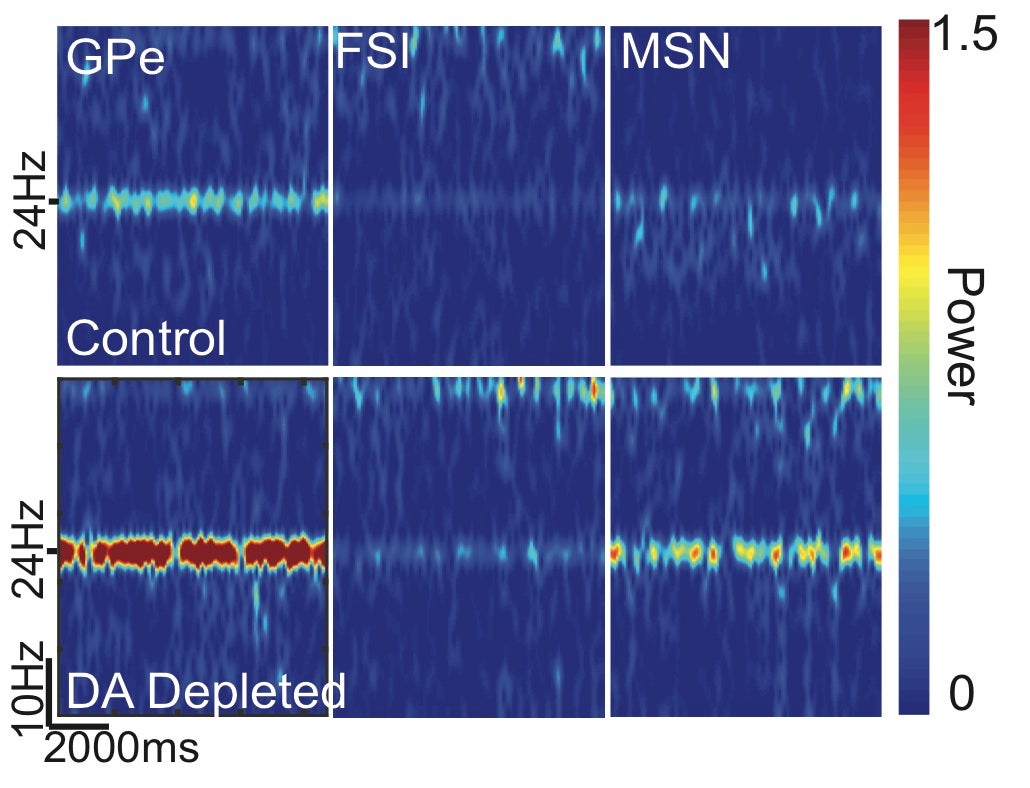 The experimental collaborator on Rubin’s CRCNS award is Dr. Aryn Gittis of the Department of Biological Sciences at Carnegie Mellon University. Dr. Gittis’s lab studies neural circuits in the basal ganglia, a brain area believed to be involved in the regulation of movement, learning, motivation, and reward. Her work emphasizes ways in which these circuits can change over time, due either to experience or to brain disorders. The grant awarded to Rubin and Gittis will support their research related to a specific brain disorder: Parkinson’s disease. It is known that Parkinson’s results from the death of cells in the basal ganglia that release a specific chemical, dopamine, associated with reward. Past studies, including work done separately by Rubin and Gittis, have also shown that neural activity and communication between neurons in the basal ganglia are altered when dopamine is lost. A central focus of their CRCNS project is to study the role of a specific, recently identified circuit in generating and maintaining runaway neural oscillations in Parkinson’s disease. This aim will be achieved via the integration of in vivo and in vitro physiological approaches together with computational model development, simulation, and mathematical analysis. A better understanding of the mechanisms underlying pathological activity in the basal ganglia may lead to the identification of targets that can be modulated to disrupt it, offering the possibility of new treatments for related motor conditions.
The experimental collaborator on Rubin’s CRCNS award is Dr. Aryn Gittis of the Department of Biological Sciences at Carnegie Mellon University. Dr. Gittis’s lab studies neural circuits in the basal ganglia, a brain area believed to be involved in the regulation of movement, learning, motivation, and reward. Her work emphasizes ways in which these circuits can change over time, due either to experience or to brain disorders. The grant awarded to Rubin and Gittis will support their research related to a specific brain disorder: Parkinson’s disease. It is known that Parkinson’s results from the death of cells in the basal ganglia that release a specific chemical, dopamine, associated with reward. Past studies, including work done separately by Rubin and Gittis, have also shown that neural activity and communication between neurons in the basal ganglia are altered when dopamine is lost. A central focus of their CRCNS project is to study the role of a specific, recently identified circuit in generating and maintaining runaway neural oscillations in Parkinson’s disease. This aim will be achieved via the integration of in vivo and in vitro physiological approaches together with computational model development, simulation, and mathematical analysis. A better understanding of the mechanisms underlying pathological activity in the basal ganglia may lead to the identification of targets that can be modulated to disrupt it, offering the possibility of new treatments for related motor conditions.
The CRCNS grant awarded to Doiron supports his longstanding collaboration with Dr. Anne-Marie Oswald of the Department of Neuroscience at the University of Pittsburgh. Dr. Oswald studies the wiring between neurons in the olfactory cortex - the area of the brain that is responsible for odor representation (sense of smell). The CRCNS grant focuses on using new genetic technology that allows scientists to probe neural circuits with light. Dr. Oswald’s lab uses these techniques to uncover how neurons that inhibit other neurons both connect to principle cells that carry odor information as well as to other inhibitory neurons. Dr. Doiron has developed models of brain circuits where these inhibitory connections serve very important roles in cortical processing, however the application has previously focused on visual and touch processing. The project aims to gather the necessary circuit information from experiments and apply these models to the specific case of olfaction. Oswald and Doiron hypothesize that there will be big differences in how inhibition shapes olfactory codes compared to its role in, for example vision. This is because the representation of odor is more analogous to how memory works in the hippocampus, making olfaction an exciting area to investigate neural codes.
New Research Grants
Free Boundary Problems and Interfacial Dynamics
Pricipal Investigator: Xinfu Chen
Sponsor: NSF
The research studies free boundary problems such as freezing of liquids, solidification of crystal, optimal investment and consumption strategy, etc. It ranges various kinds of areas from industry to finance. Theoretical study will be focused on interfacial dynamics.
Predictive Mathematical Models of Inflammation
Principal Investigator: Gregory Constantine
Sponsor : NIH
The aims of this project are: 1) To utilize gene-modified mice and cells, multiplexed analyte data, statistical methods, and multi-scale simulations of the inflammatory response in order to discern master switches that might be modified therapeutically; 2) To define in silico the in vitro and in vivo roles of DAMP’s and their receptors in the phenomenon of preconditioning; and 3) To create patient-specific and population simulations of the human inflammatory response to trauma that include both plasma analyte dynamics and cytokine single nucleotide polymorphisms, coupled to in silico clinical trials.
Numerical Analysis of Non-Equilibrium Turbulence
Principal Investigator: William Layton
Sponsor: NSF
Complex turbulence not at statistical equilibrium occurs in almost all engineering flows. Its accurate simulation is essential for many critical applications including global change estimation and energy efficiency optimization. For example, 85% of the energy in the US is generated by combustion for which understanding turbulent mixing is critical: energy efficiency optimization requires accurate simulation of turbulent mixing. The research in this grant treats turbulence not at statistical equilibrium. Unfortunately, there is little mathematical theory, applicable physical phenomenology, effective models or systematic computational practice for this case. The goal of the research is to extend models and algorithms to turbulence not at statistical equilibrium allowing for backscatter (energy flow from fluctuations back to means) without negative viscosities and to develop a rigorous numerical analysis of the new models and algorithms. One theme is to study how to take a model that is accepted for statistically steady turbulence in a specific application and setting and show how to adapt that model to complex turbulence in a mathematically sound and physically lucid manner.
Nonlinear PDEs, Numerical Analysis, and Applications
Principal Investigator: Michael Neilan
Sponsor: NSF
This conference creates a forum for junior and senior researchers to discuss challenges and to disseminate recent advances on numerical methods for fully nonlinear PDEs and their applications. Impacts of the conference include:
(i) Exposing graduate students and postdocs to the relatively new, yet active field of numerical non-linear PDEs. The conference provides an informal setting in which young researchers and leading experts in numerical analysis can meet, collaborate, and develop new ideas. (ii) Defining and discussing critical open problems in the field. Talks by mid-to-senior level experts in numerical analysis outline recent results and the barriers that must be overcome to enable new results. (iii) Providing a valuable academic resource to students in the western Pennsylvania region. Western PA is the home to several universities with active graduate programs in computational mathematics (e.g., University of Pittsburgh, Carnegie Mellon, Duquesne University). Specifically at the University of Pittsburgh, the themes of this conference overlap many of the graduate students' research areas. In addition, the conference provides a service to the University of Pittsburgh and the surrounding region by bringing recognition to the university in regards to its efforts in this research area.
Large Eddy Simulations in Magnetohydrodynamics Flows
Principal Investigator: Catalin Trenchea
Sponsor: NSF
Magnetohydrodynamics describes the behavior of an electrically conducting fluid flow in the presence of magnetic fields. Electrically conducting fluids arise in applications including astrophysics, geophysics, plasma confinement, controlled thermonuclear fusion, liquid-metal cooling of nuclear reactors, electromagnetic casting of metals, ion thrusters for low orbiting satellites, magnetohydrodynamic drive for ships and submarines, microfluidic devices, and molecular biology. The fluid motion of the Earth's core maintains the terrestrial magnetic field, the solar magnetic field generates sunspots and solar flares, and the galactic magnetic field influences the formation of stars from interstellar clouds. These applications require substantially better modeling and simulation capabilities than presently exist. Problems without a clear scale separation, such as turbulence, are still at the frontier of multiscale modeling and simulation. When the fluid is electrically conducting, the turbulent fluid motions are accompanied by magnetic fluctuations. For Magnetohydrodynamic (MHD) turbulence, numerical simulations play a greater role than they play for hydrodynamic turbulence, since laboratory experiments are practically impossible and astrophysical systems (solar-wind turbulence, the most important system of high-Reynolds-number MHD accessible to in situ measurements) are too complex to be comparable with theoretical results. This research project will develop improved computational methods for these important problems.
This research project studies mathematically rigorous and computationally efficient methods to analyze direct and inverse problems constrained by MHD models. This includes the numerical analysis of computational algorithms, implicit explicit time-stepping schemes using the Elsasser variables, post processing via time-filters, spatial linear and nonlinear filters, spectral filtering, development of spatial filters specific to MHD turbulence, optimal control, and parameter estimation. Another objective of this project is to investigate the mathematical properties of several models for the simulation of the large eddies in turbulent viscous, incompressible, electrically conducting flows and new numerical models that permit long-time simulations, by time-splitting. The project has a broad impact for training undergraduate and graduate students in analytical and numerical aspects of magnetohydrodynamics, turbulence, and inverse problems.
Nonlinear Waves in Nonintegrable Lattices
Principal Investigator: Anna Vainchtein
Sponsor: NSF
Many physical and biological systems are both spatially discrete and nonlinear. Examples include crystal lattices, biopolymers, and nanoelectromechanical devices. The interplay of the discrete structure and nonlinearity often leads to the formation of spatially localized nonlinear waves that carry or trap energy. This project will advance fundamental understanding of properties and stability of nonlinear waves in discrete structures, which is important in a number of different fields, including materials science, condensed matter physics, mechanical engineering, and biophysics. It will also provide insight into the dynamics of nonlinear waves in two new types of tunable granular metamaterials and develop novel approaches to channeling and trapping of acoustic energy, with potential applications to energy harvesting, shock absorption, and vibration mitigation. An integral component of the project is teaching and training graduate students in the interdisciplinary research area of nonlinear lattice dynamics.