Advanced calculus + Sard's Theorem = Lots of Topology!

Differential topology studies smooth manifolds and smooth maps between them. If $f: M\rightarrow N$ is a smooth map between $m$- and $n$-dimensional manifolds, then the fundamental theorem of Sard asserts that generically the pre-image of a $y\in N$ is an $m-n$ dimensional submanifold of $M$.

 

It turns out that properties of these pre-images can reveal surprisingly significant amount of information about the underlying topology of the spaces, and the mappings between them. In this regard, I will define for a map between manifolds of the same dimension, the degree mod $2$, and then the degree. These already are sufficient to prove some interesting results of topology (e.g. Brouwer's fixed-point theorem, fundamental theorem of algebra, nonexistence of nowhere zero vector fields on even spheres, etc.)

However, the real surprise is the "framed cobordism", which establishes a 1-1 correspondence between classes of submanifolds of $M$, and homotopy classes of maps $f:M\rightarrow S^p$, (the sphere.) 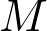 need not be of the same dimension as $S^p$.

I will try to reproduce the detailed and lucid proofs of the Milnor's book "Topology from the Differentiable Viewpoint," because they have a number of thematic ideas and tricks that can come in handy for anyone dealing with topology!